Hello Murray,
I wanted to ask you a strange question that I found it little weird.. When we first learned about square roots we had never encountered complex numbers, so the only objects that had sqare roots were positive numbers. In this case, sqrt(a/b) = sqrt(a) / sqrt(b) is always true .. But it fails to remain true after we extend the definition of "square root" to allow the square roots of negative and complex numbers.
Where the correct rule was
sqrt(a/b) = + or - sqrt(a) / sqrt(b)
Same thing for
sqrt(a*b) = + or - sqrt(a) * sqrt(b)
If a and b are positive real numbers the equation with a + sign will take its place!
This happened when we tried to calculate the following(attachment):
**Notice the minus that must be included somtimes .. so the question is : Are there any logical explanation for when we must have - or + ?? Or it just had to be randomly taken and wish it would be true?
Hello Murray,
I wanted to ask you a strange question that I found it little weird.. When we first learned about square roots we had never encountered complex numbers, so the only objects that had sqare roots were positive numbers. In this case, sqrt(a/b) = sqrt(a) / sqrt(b) is always true .. But it fails to remain true after we extend the definition of "square root" to allow the square roots of negative and complex numbers.
Where the correct rule was
sqrt(a/b) = + or - sqrt(a) / sqrt(b)
Same thing for
sqrt(a*b) = + or - sqrt(a) * sqrt(b)
If a and b are positive real numbers the equation with a + sign will take its place!
This happened when we tried to calculate the following(attachment):
<img src="/forum/uploads/imf-4733-screenshot2016-07-03-03-57-09-1.png" width="206" height="205" alt="complex-numbers" />
**Notice the minus that must be included somtimes .. so the question is : Are there any logical explanation for when we must have - or + ?? Or it just had to be randomly taken and wish it would be true?
Relevant page
<a href="https://www.physicsforums.com/threads/sqrt-1-sqrt-1.571842/">Sqrt (-1) * sqrt (-1) | Physics Forums - The Fusion of Science and Community</a>
What I've done so far
(Work included as a photo in the Question!)
Now to the equations in your image. (You are encouraged to use the math entry system - it makes it easier to discuss.)
For the first 2, neither statement is correct because by convention, we multiply under the square root first. (See Examples 3d and 3e on this page: 1. Basic Definitions of Complex Numbers)
For your 3rd and 4th equations, once again neither is correct because we should multiply under the square root first.
So it should be:
`sqrt(i^3) = sqrt(-i)`
Now, that provides us with a challenge. We'll need to use DeMoivre's theorem:
`-i = cos((3pi)/2) + i sin((3pi)/2)`
`sqrt(-i) = (cos((3pi)/2) + i sin((3pi)/2))^(1/2)`
`= cos((3pi)/4) + i sin((3pi)/4)`
`= (-1+i)/sqrt(2)`
Do you think you can sort out your last 3 equations now?
X
Hello Nour
It's good you are asking such questions - mathematics is not always as consistent as (some) math teachers make it out to be.
Some of these issues also came up in Rika's post, here: <a href="https://staging.intmath.com/forum/exponents-radicals-16/rules-for-radicals:35">Rules for radicals</a>
The main problem is we should always define the conditions for such expressions to be true.
You wrote
`sqrt(a/b) = sqrt(a) / sqrt(b)` is always true.
Well, only if `a>0`, `b>0`.
You then said:
`sqrt(a/b) = +- sqrt(a) / sqrt(b)`
`sqrt(a*b) = +- sqrt(a) * sqrt(b)`
Actually, these 2 are not correct. A square root only gives us <b>one</b> positive result.
See this (and the discussion following):
<a href="https://staging.intmath.com/blog/mathematics/square-root-16-how-many-answers-122">sqrt(16) - how many answers?</a>
Now to the equations in your image. (You are encouraged to use the <a href="https://staging.intmath.com/forum/entering-math-graphs-images-41/how-to-enter-math:91">math entry system</a> - it makes it easier to discuss.)
For the first 2, neither statement is correct because by convention, we multiply under the square root first. (See Examples 3d and 3e on this page: <a href="/complex-numbers/1-basic-definitions.php">1. Basic Definitions of Complex Numbers</a>)
For your 3rd and 4th equations, once again neither is correct because we should multiply under the square root first.
So it should be:
`sqrt(i^3) = sqrt(-i)`
Now, that provides us with a challenge. We'll need to use <a href="https://staging.intmath.com/complex-numbers/7-powers-roots-demoivre.php">DeMoivre's theorem</a>:
`-i = cos((3pi)/2) + i sin((3pi)/2)`
`sqrt(-i) = (cos((3pi)/2) + i sin((3pi)/2))^(1/2)`
`= cos((3pi)/4) + i sin((3pi)/4)`
`= (-1+i)/sqrt(2)`
Do you think you can sort out your last 3 equations now?
1) Murray: "you wrote ` sqrt(a/b) = sqrt(a)/sqrt(b)` .well, only if `a>0` and `b>0` "
To be more precise, it is `a>= 0` .
Anyway, that's exactly what i said ,notice the expressions "In this case, .." and "If a and b are positive real numbers .." where I mentioned those two conditions.
2) Murray: "A square root only gives us one positive result."
Notice that I mentioned " + or - " there is always one solution, but it could be either this or this. And those aren't actually a given for square roots, these are expressions before square rooting (before evaluation square root).
However, `sqrt(16)` is a very different case, alot of people don't know that for a real number 'a' we have
`sqrt(a^2) = |a| ` not `a`.
For example,
`a^2 = 4`
Square-root both sides,
`sqrt(a^2) = sqrt(4)`
`|a| = 2`
This leaves us with `a=2` or `a=-2`
That's why we put `+-` it is all a matter of logic.
? `sqrt(2^2) = 2`
? `sqrt((-2)^2) = |-2| = 2`
Now this always has to give one positive result and not the earlier expression!
3) Murray : "because by convention, we multiply under the square root first."
Well, yes ofcourse but this was just to show the rule that `sqrt(a×b) = - sqrt(a) × sqrt(b)` for `a,b<=0` .
4) Murray : " We'll need to use DeMoivre's theorem"
Mmmm, DeMoivre's theorem is only applicable for either 'real non-decimal indexes with any angle' , or 'any index but with angle between 0 and `pi` regardless of the sign.
Your result returned wrong because you used `(3 pi)/2` instead of using ` (- pi) /2` (the second condition is used ~~ any index with angle less than `pi`).
If you tries the following indexes with any angle,
0 1 5 8 -4 -6 -1 -2 ...
You'll see that DeMoivre's theorem is correct!
However, trying the following indexes,
-1.2 3.5 `1/2` `-2/3` 2i -3i ...
Will lead to false results. You would notice that, ` 1/2` and `-1/2` are special indexes where the result is just multiplied by (-1).
You can try for yourself,
Here I tried x=-2.6 ,
5) Your result is not true and `sqrt(-i) != (-1+i)/sqrt(2)`.
You just said from Rika's post that m and n must be integers. And by using wolfram alpha we get,
----------
Well actually I understand it know!
I just had to transform the complex number to the exponent form and fix the angle to be less than `pi` so then the result will be true :D thank you very much, this was really helping me. And here's the result:
`sqrt(-i) = sqrt( e^(- pi/2 i) ) =`
`e^((- pi/2 i)×(1/2)) = e^(- pi/4 i) = `
` (1-i)/sqrt(2)` Correct!
Thanks again :)
X
Hello again,
1) Murray: "you wrote ` sqrt(a/b) = sqrt(a)/sqrt(b)` .well, only if `a>0` and `b>0` "
To be more precise, it is `a>= 0` .
Anyway, that's exactly what i said ,notice the expressions "In this case, .." and "If a and b are positive real numbers .." where I mentioned those two conditions.
2) Murray: "A square root only gives us one positive result."
Notice that I mentioned " + or - " there is always one solution, but it could be either this or this. And those aren't actually a given for square roots, these are expressions before square rooting (before evaluation square root).
However, `sqrt(16)` is a very different case, alot of people don't know that for a real number 'a' we have
`sqrt(a^2) = |a| ` not `a`.
For example,
`a^2 = 4`
Square-root both sides,
`sqrt(a^2) = sqrt(4)`
`|a| = 2`
This leaves us with `a=2` or `a=-2`
That's why we put `+-` it is all a matter of logic.
? `sqrt(2^2) = 2`
? `sqrt((-2)^2) = |-2| = 2`
Now this always has to give one positive result and not the earlier expression!
3) Murray : "because by convention, we multiply under the square root first."
Well, yes ofcourse but this was just to show the rule that `sqrt(a×b) = - sqrt(a) × sqrt(b)` for `a,b<=0` .
4) Murray : " We'll need to use DeMoivre's theorem"
Mmmm, DeMoivre's theorem is only applicable for either 'real non-decimal indexes with any angle' , or 'any index but with angle between 0 and `pi` regardless of the sign.
Your result returned wrong because you used `(3 pi)/2` instead of using ` (- pi) /2` (the second condition is used ~~ any index with angle less than `pi`).
If you tries the following indexes with any angle,
0 1 5 8 -4 -6 -1 -2 ...
You'll see that DeMoivre's theorem is correct!
However, trying the following indexes,
-1.2 3.5 `1/2` `-2/3` 2i -3i ...
Will lead to false results. You would notice that, ` 1/2` and `-1/2` are special indexes where the result is just multiplied by (-1).
You can try for yourself,
Here I tried x=-2.6 ,
<img src="/forum/uploads/imf-5729-screenshot2016-07-04-09-50-09-1.png" width="230" height="219" alt="complex-numbers" />
5) Your result is not true and `sqrt(-i) != (-1+i)/sqrt(2)`.
You just said from Rika's post that m and n must be integers. And by using wolfram alpha we get,
<img src="/forum/uploads/imf-1026-screenshot2016-07-04-10-09-32-1.png" width="239" height="211" alt="complex-numbers" />
----------
Well actually I understand it know!
I just had to transform the complex number to the exponent form and fix the angle to be less than `pi` so then the result will be true :D thank you very much, this was really helping me. And here's the result:
`sqrt(-i) = sqrt( e^(- pi/2 i) ) =`
`e^((- pi/2 i)×(1/2)) = e^(- pi/4 i) = `
` (1-i)/sqrt(2)` Correct!
Thanks again :)
(1) Yes, you are correct, it should have been `a>=0` and `b>0`.
(2) Actually, no we don't put `+-` when it says square root. there is only one principle square root, and it's positive.
(3) `sqrt(axxb)=sqrt(a)xxsqrt(b)` if `a>=0`, `b>=0`. If either `a` or `b` is negative, we don't get `-sqrt(a)xxsqrt(b)`
(4) Hmm - yes I jumped into using deMoivre's without considering its conditions. Naughty me.
But I didn't question my result further because it gives a correct answer, since
`((-1+i)/sqrt(2))^2 = -i`, which is what we want.
Your result also gives the correct answer when multiplied out:
`((1-i)/sqrt(2))^2 = -i`
Wolfram|Alpha gives both answers, yours as a "principle" root, and mine as another root:
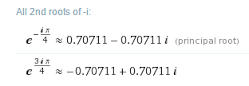
So in a sense, I've done exactly what I've said not to do with `sqrt(16)` - I've found the non-principle negative root. Thanks for pointing it out.
I'm glad you've got a handle on it now!
All the best.
X
(1) Yes, you are correct, it should have been `a>=0` and `b>0`.
(2) Actually, no we don't put `+-` when it says square root. there is only one principle square root, and it's positive.
(3) `sqrt(axxb)=sqrt(a)xxsqrt(b)` if `a>=0`, `b>=0`. If either `a` or `b` is negative, we don't get `-sqrt(a)xxsqrt(b)`
(4) Hmm - yes I jumped into using deMoivre's without considering its conditions. Naughty me.
But I didn't question my result further because it gives a correct answer, since
`((-1+i)/sqrt(2))^2 = -i`, which is what we want.
Your result also gives the correct answer when multiplied out:
`((1-i)/sqrt(2))^2 = -i`
Wolfram|Alpha gives both answers, yours as a "principle" root, and mine as another root:
<img src="/forum/uploads/imf-5215-principle.png" width="249" height="86" alt="complex-numbers" />
So in a sense, I've done exactly what I've said not to do with `sqrt(16)` - I've found the non-principle negative root. Thanks for pointing it out.
I'm glad you've got a handle on it now!
All the best.
It's interesting to see your approach to finding the square root of a complex number using polar coordinates. Your calculation for (2+3i)^2 = -5+12i seems correct, and your conversion into polar form with theta = 0.5880 is on point. Have you considered exploring the concept of principal square roots in complex numbers further? It might shed more light on how to determine the correct square root when dealing with complex numbers. Keep up the good work in unraveling the mysteries of complex arithmetic!
X
It's interesting to see your approach to finding the square root of a complex number using polar coordinates. Your calculation for (2+3i)^2 = -5+12i seems correct, and your conversion into polar form with theta = 0.5880 is on point. Have you considered exploring the concept of principal square roots in complex numbers further? It might shed more light on how to determine the correct square root when dealing with complex numbers. Keep up the good work in unraveling the mysteries of complex arithmetic!
@geometry dash It seems like you're exploring the idea of representing integers as the sum of complex numbers with specific arguments. Murray's point about showing your working is crucial for pinpointing where the challenge lies. Have you tried breaking down how to express those 11 integers using complex numbers with angles of 45°, 135°, and 270°? It might be a fascinating exercise to work through examples to see if patterns emerge based on these arguments. Exploring different approaches step by step could shed light on this intriguing concept further.
X
@<a href="https://geometrydashfullversion.io/">geometry dash</a> It seems like you're exploring the idea of representing integers as the sum of complex numbers with specific arguments. Murray's point about showing your working is crucial for pinpointing where the challenge lies. Have you tried breaking down how to express those 11 integers using complex numbers with angles of 45°, 135°, and 270°? It might be a fascinating exercise to work through examples to see if patterns emerge based on these arguments. Exploring different approaches step by step could shed light on this intriguing concept further.
@Geometry Dash Ah, this is a really good observation — you’ve stumbled into one of the subtleties of extending the square root function beyond positive real numbers. Let’s unpack it carefully.
X
@<a href="https://geometry-dashonline.io">Geometry Dash</a> Ah, this is a really good observation — you’ve stumbled into one of the subtleties of extending the square root function beyond positive real numbers. Let’s unpack it carefully.
@Dinosaur Game
For positive real numbers, the square root is unique, so identities like
√(a/b) = √a / √b and √(ab) = √a·√b always hold.
When extended to negative and complex numbers, every nonzero number has two square roots (±), so the square root becomes multi-valued.
Because of this, those identities no longer hold in general; the correct form is
√(ab) = ±√a·√b and √(a/b) = ±√a / √b.
The ± sign is not random—it depends on which branch of the square root is chosen.
To avoid ambiguity, mathematics defines the principal square root, but then some familiar multiplication and division rules must be abandoned.
Conclusion: The failure of square-root rules in complex numbers is not a contradiction; it happens because square roots are inherently two-valued, so you cannot keep all real-number identities at the same time.
X
@<a href="https://dinosaur-game.io/">Dinosaur Game</a>
For positive real numbers, the square root is unique, so identities like
√(a/b) = √a / √b and √(ab) = √a·√b always hold.
When extended to negative and complex numbers, every nonzero number has two square roots (±), so the square root becomes multi-valued.
Because of this, those identities no longer hold in general; the correct form is
√(ab) = ±√a·√b and √(a/b) = ±√a / √b.
The ± sign is not random—it depends on which branch of the square root is chosen.
To avoid ambiguity, mathematics defines the principal square root, but then some familiar multiplication and division rules must be abandoned.
Conclusion: The failure of square-root rules in complex numbers is not a contradiction; it happens because square roots are inherently two-valued, so you cannot keep all real-number identities at the same time.
The rhythm-based arcade game Space Waves combines futuristic graphics, music, and reflexes into one thrilling experience. Although the game appears straightforward at first, you soon discover how difficult and captivating it can be once you start playing.
X
The rhythm-based arcade game <a href="https://spacewavesonline.io/">Space Waves</a> combines futuristic graphics, music, and reflexes into one thrilling experience. Although the game appears straightforward at first, you soon discover how difficult and captivating it can be once you start playing.
Discover exciting options with top online casino games Pakistan players love.
Enjoy smooth graphics, fair odds, and real rewards.
X
Discover exciting options with <a href="https://royalxcasinoz.pk/">top online casino games Pakistan</a> players love.
Enjoy smooth graphics, fair odds, and real rewards.
Hey Murray, great question! Diving into the complexities of square roots can feel like navigating a tricky level in Snow rider . It's fascinating how sqrt(a/b) = sqrt(a) / sqrt(b) holds true for positive numbers but requires a +/- consideration when venturing into complex numbers. Is there a logical key to unlock the correct sign, or is it more of a trial-and-error approach, hoping for the best outcome as we barrel down the virtual slopes? I'm eager to see your thoughts on this.
X
Hey Murray, great question! Diving into the complexities of square roots can feel like navigating a tricky level in <a href="https://snowridergame.io">Snow rider</a> . It's fascinating how sqrt(a/b) = sqrt(a) / sqrt(b) holds true for positive numbers but requires a +/- consideration when venturing into complex numbers. Is there a logical key to unlock the correct sign, or is it more of a trial-and-error approach, hoping for the best outcome as we barrel down the virtual slopes? I'm eager to see your thoughts on this.
Reply
You need to be logged in to reply.
Related Complex Numbers questions
INTEGRATION[Solved!] Must the differential be included ALWAYS in the integrand?
If so, then why?phinah 03 Feb 2020, 03:31
